Cách bấm máy tính hoán vị chỉnh hợp tổ hợp nhanh nhất 2022

1. Lý thuyết hoán vị chỉnh hợp tổ hợp

Trước khi khám phá về cách bấm máy tính hoán vị chỉnh hợp tổng hợp, những em cùng VUIHOC ôn tập kim chỉ nan về hoán vị chỉnh hợp tổng hợp để nắm được kiến thức và kỹ năng nền tảng trước nhé !

1.1. Hoán vị

Định nghĩa: Cho tập hợp A bao gồm n phần tử (n>=1). Cách sắp thứ tự n phần tử của tập hợp A được gọi là hoán vị của n phần tử thuộc tập A.

Bạn đang đọc: Cách bấm máy tính hoán vị chỉnh hợp tổ hợp nhanh nhất 2022

Công thức hoán vị : Pn = n ! = 1.2.3 … ( n − 1 ). n
Kí hiệu hoán vị của n thành phần : Pn

Ví dụ : Cho tập A = { 3, 4, 5, , 6, 7 }. Từ tập A hoàn toàn có thể lập được bao nhiêu số gồm 5 chữ số phân biệt ?
Giải : P5 = 5 ! = 120 số .

1.2. Chỉnh hợp

Định nghĩa : Cho tập hợp A gồm n thành phần. Một bộ gồm k ( 1 < = k < = n ) thành phần được sắp xếp thứ tự của tập hợp A được gọi là một chỉnh hợp chập k của n thành phần của tập A . Công thức :

Kí hiệu chỉnh hợp chập k của n thành phần : Ank
Ví dụ : Có bao nhiêu cách xếp ba khách Minh, Thông, Thái vào hai chỗ ngồi cho trước ?
Giải :

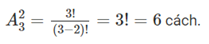
1.3. Tổ hợp
Định nghĩa: Cho tập hợp A gồm n phần tử. Trong tập con của A bao gồm k phần tử phân biệt (1 <= k <= n), được gọi là một tổ hợp chập k của n phần tử của A.

Tổ hợp và chỉnh hợp thường hay bị những bạn học viên nhầm lẫn với nhau. Sau đây là 2 sự độc lạ cơ bản của tổng hợp và chỉnh hợp :

• Chỉnh hợp là bộ sắp có thứ tự : ví dụ, { a, b, c }, { a, c, b }, …
• Tổ hợp là bộ sắp không có thứ tự : ví dụ, { a, b, c } – > đúng. Trong khi đó { a, c, b } và những cách sắp thứ tự kiểu khác của { a, b, c } không được tính là tổng hợp .

Các công thức tổng hợp ( k, n thỏa mãn nhu cầu điều kiện kèm theo xác lập ) :

Ví dụ về tổng hợp : Ông X có 11 người bạn. Ông ta muốn mời 5 người trong số họ đi chơi xa. Trong 11 người đó có 2 người không muốn gặp mặt nhau. Hỏi ông X có bao nhiêu cách mời ?
Giải : 2 * C94 + C95 = 2 * 126 + 126 = 252 + 126 = 378 cách
Giải thích cụ thể :
+ Ông X chỉ mời 1 trong 2 người bạn không muốn gặp nhau và mời thêm 4 trong số 9 người còn lại : 2 * C94 = 252
+ Ông X không mời ai trong 2 người bạn không muốn gặp nhau mà chỉ mời 5 trong số 9 người kia : C95 = 126

2. Cách bấm máy tính hoán vị chỉnh hợp tổ hợp

2.1. Giai thừa

Giai thừa là tích của n số tự nhiên liên tục kể từ 1 và được ký hiệu n !. Công thức tính giai thừa là n ! = 1.2.3 … n .
Cùng tìm hiểu và khám phá cách bấm máy tính hoán vị chỉnh hợp tổ hợp phần giai thừa trong ví dụ sau đây :

Ví dụ: Tính kết quả của 6!.

Bước 1: Nhập số 6 > Chọn SHIFT > Chọn $x^{ -1}$.

Bước 2: Nhấn dấu = để xem kết quả.

 

Xem thêm: TOP 5 Laptop màn hình cảm ứng chất lượng, giá tốt nên mua 2023 | Nguyễn Kim | Nguyễn Kim Blog

2.2. Hoán vị

Cách bấm máy tính hoán vị được mô phỏng trong ví dụ sau đây :

Ví dụ: Hỏi có bao nhiêu cách để sắp xếp 4 người vào băng ghế có 4 chỗ?

Bước 1: Lúc này Pn = 4! nên ta nhập 4 vào máy tính > Chọn SHIFT > Chọn $x^ {-1}$.

Bước 2: Nhấn dấu = để xem kết quả > Có 24 cách để sắp xếp.

 

2.3. Chỉnh hợp

Tương tự với cách bấm máy tính hoán vị chỉnh hợp tổng hợp, ta cũng xét ví dụ sau đây để hiểu cách tính chỉnh hợp bằng máy tính :

Ví dụ: Sắp xếp 6 người vào băng ghế có 8 chỗ ngồi.

Để tính được ví dụ trên ta bấm như sau :

Bước 1: Nhập số 8 vào máy > Chọn SHIFT > Chọn dấu nhân.

’

Bước 2: Nhập vào số 6 > Nhấn dấu =.

2.4. Tổ hợp

Đối với tổng hợp, ta xét ví dụ sau đây :
Ví dụ : Một lớp học có 30 học viên. Hỏi có bao nhiêu cách để chọn ra 2 học viên làm ban cán sự lớp ?
Để giải bài toán trên bằng máy tính cầm tay ta thực thi như sau :

Bước 1: Nhập vào máy 30 > Chọn phím SHIFT > Chọn dấu chia.

Bước 2: Nhập 2 vào máy > Chọn dấu =.

 

3. Áp dụng cách bấm máy tính hoán vị chỉnh hợp tổ hợp giải các bài tập xác suất

Trong phần này, những em học viên cùng VUIHOC vận dụng cách bấm máy tính hoán vị chỉnh hợp tổng hợp để giải nhanh những bài tập Phần Trăm sau đây. Lưu ý, những em nên sử dụng máy tính bấm ra hiệu quả, sau đó giải bằng cách tự luận thường thì để kiểm tra tác dụng nhé !

Bài toán 1: Có bao nhiêu số tự nhiên có ba chữ số đôi một khác nhau được lập từ các chữ số 1, 2, 3, 4, 5?

Bài toán 2: Một lớp học có có 27 học sinh trong đó có 12 nam và 15 nữ. Hỏi cách bao nhiêu cách để chọn 1 nhóm gồm 2 nam và 2 nữ?

Bài toán 3: Có 2 dãy ghế, mỗi dãy có 5 chỗ ngồi. Xếp 5 nam, 5 nữ vào hai dãy ghế trên. Hỏi có bao cách xếp sao cho nam và nữ được xếp tùy ý?

 

Xem thêm: Các cách quay màn hình máy tính, laptop cực chi tiết

Bài toán 4: Trong không gian, cho tập hợp X gồm 10 điểm, trong đó không có ba điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác được tạo thành?

Bài viết trên đã tổng hợp lý thuyết chung về hoán vị chỉnh hợp tổng hợp và hướng dẫn cách bấm máy tính hoán vị chỉnh hợp tổng hợp. Hy vọng rằng những giải pháp giải CASIO trên sẽ giúp những em học viên tiết kiệm chi phí thời hạn khi giải những bài tập Phần Trăm trong chương trình học. Để đọc nhiều hơn những bài viết khác về Toán trung học phổ thông, Toán lớp 10, … những em truy vấn vuihoc.vn hoặc ĐK khóa học ngay từ ngày hôm nay nhé !

Source: https://suanha.org
Category : Máy-tinh